目的
特にしっかりした目的はない。
なんとなく数値シミュレーションについて学び直したくなったため、現在身近にある現象を題材にして学ぶ。
ネットの情報を参考に、適当にシミュレーションを走らせてみる。
※本シミュレーションは、実測値等には全く基づいていないため、完全に空想上のシミュレーションになります。
本シミュレーションの結果が実情を反映していたり、今後の予測を示していたりはしません。
今回扱うシミュレーションモデル
SEIRモデルを扱う。
SEIRモデルとは
SEIRモデル(エスイーアイアールモデル)とは感染症流行の数理モデルである。
モデルは
- 感染症に対して免疫を持たない者(Susceptible)
- 感染症が潜伏期間中の者(Exposed)
- 発症者(Infectious)
- 感染症から回復し免疫を獲得した者(Recovered)
から構成され、その頭文字をとってSEIRモデルと呼ばれる。
(Wikipediaより)
モデル式は以下のような式で表される。
$$ \begin{aligned} \frac{dS}{dt} &= m(N - S) - bSI &(1) \cr \frac{dE}{dt} &= bSI - (m + a)E &(2) \cr \frac{dI}{dt} &= aE - (m + g)I &(3) \cr \frac{dR}{dt} &= gI - mR &(4) \end{aligned} $$
ここで\(t\)は時間、\(m\)は出生率及び死亡率、\(a\)は感染症の発生率、\(b\)は感染症への感染率、\(g\)は感染症からの回復率を表す。
また\(N\)は全人口を示し、
$$N \equiv S + E + I + R (5)$$
で定義される。
この式をみて、以前私が扱ったことのある、化学反応モデルにおける各化学種の質量分率の計算式に似てるなと思った。
化学反応も逐次的に進行するし、感染も未感染から回復まで逐次的に進行するから、モデル的には同じような扱いになるのだろうか。
全体的に構成はシンプルだが、一つ気になったのは(1)式右辺の項bSIについて。
この項は非感染者と感染者の接触によってSusceptibleの人がExposedになる振る舞いを表しているのだと思う。
ここで接触率とかは対象の環境によるのだと思うのだが、式上では接触率のようなものは出てこない。
パラメータbにそこらへんも含まれているのかもしれないが、ここら辺はもう少し調べないと分からないなと思った。
計算してみる
上の式を数値的に解いてみる。
シミュレーションを行う前に、上の式を少し修正し、適当にパラメータを決める。
式を修正する
上の式はあくまで定義式なので、計算しやすいように、また、今回取り扱う問題に合うように修正する。
修正する内容は以下の資料を参考にさせていただく。
http://www.bs.s.u-tokyo.ac.jp/content/files/covid/COVID-19_SEIRmodel_full_ver4.1.pdf
今回は扱うモデル式を以下のようにする。
$$ \begin{aligned} \frac{dS}{dt} &= -(\frac{R_0}{i})\frac{S}{N}I &(6) \cr \frac{dE}{dt} &= -(\frac{R_0}{i})\frac{S}{N}I - (\frac{1}{l})E &(7) \cr \frac{dI}{dt} &= (\frac{1}{l})E - (\frac{1}{i})I &(8) \cr \frac{dR}{dt} &= (\frac{1}{i})I &(9) \end{aligned} $$
ここで、\(R_0\)は基本再生産数、\(l\)は平均潜伏期間、\(i\)は平均発症期間である。
wikipediaの式と比べて変わったところは、
- 出生・死亡については無視する
- 各パラメータについて、基本再生産数、平均潜伏期間、平均発症期間から与えられるように式を変形
なお、ここでの式変形については参考元のページに非常に分かりやすい説明があるため、そちらを参照いただきたい。
パラメータを決める
モデル式が決まったので、パラメータを決める。
今回、式に含まれるパラメータは\(R_0\)、\(l\)、\(i\)の値、及び\(S\)、\(E\)、\(I\)、\(R\)の初期値である。
\(R_0\)、\(l\)、\(i\)はネットの情報をもとにそれっぽい値に設定する。
\(R_0\)を決める
今回のモデル式においては、このパラメータには人と人との接触率みたいなものも含まれるので、最も重要になると思う。
基本再生産数について改めて調べてみると色々な調査結果がある。
2月12日に公開されている論文1によると、1.4から6.49まで調査結果に開きがあるらしい。
それぞれ調査期間や場所、方法が違うため当然なのだが、今回はWHOが1月18日に調査したらしい結果、1.4-2.5(平均1.95)という結果を参考にする。
とりあえず平均の1.95と、この値の変化による全体の傾向の変化をつかむため、1.5の場合と3.0の場合も計算しておく。
\(l\)を決める
平均潜伏期間について調査する。
これについても様々な調査結果が報告されている。
Johns Hopkins Bloomberg School of Public Healthの調査2によると、
There were 181 confirmed cases with identifiable exposure and symptom onset windows to estimate the incubation period of COVID-19. The median incubation period was estimated to be 5.1 days (95% CI, 4.5 to 5.8 days), and 97.5% of those who develop symptoms will do so within 11.5 days (CI, 8.2 to 15.6 days) of infection.
とあり、感染から発症までの潜伏期間の中央値は5.1日らしい。
日本感染症学会のページ3には、
潜伏期間は1~14日で平均5.8日と報告されている。
と書かれている。
日本国内の自治体の報告例としては、福井県が、県内の罹患者のうち、潜伏期間が推定できたケースの平均値は5.2日であると報告4している。
これらの報告例から、今回の平均潜伏期間$l$はとりあえず5日と設定する。
\(i\)を決める
平均発症期間について調査する。
WHOの中国における調査結果5によると、
Using available preliminary data, the median time from onset to clinical recovery for mild cases is approximately 2 weeks and is 3-6 weeks for patients with severe or critical disease. Preliminary data suggests that the time period from onset to the development of severe disease, including hypoxia, is 1 week. Among patients who have died, the time from symptom onset to outcome ranges from 2-8 weeks.
とあり、軽症の場合は約2週間、重症以上の場合は3~6週間かかるらしい。
国内の報告例としては国立感染症研究所が
入院開始日と退院日ともに判明している102例における入院期間の平均値(標準偏差)は14.3日(±5.2日)であった。
と報告6している。
これらの報告例から、今回の平均発症期間$i$はとりあえず14日と設定する。
\(S\),\(E\),\(I\),\(R\)の初期値を決める
これは今回の本質とはあまり関係ないと思われる。
とりあえず\(S\)の初期値は東京都の人口13,951,636人(令和2年1月1日推計7)に設定し、\(I\)の初期値は1、他の初期値は0にする。
よって、東京都に一人の感染者がいる状態を初期状態とする。(もちろん都道府県間の人の移動は今回考慮しない。)
プログラムを作成する
pythonで書く。
この方程式は時間微分しかないためエクセルでも数値的に解けるが、勉強のためpythonを使ってみる。
とくに急峻な値の変化はなさそうなので、数値安定性とかを気にする必要はなさそうだが、せっかくなので数値解析してる風にするため、時間発展手法には4段4次陽的ルンゲクッタ法を使う。
4段4次陽的ルンゲクッタ法の計算式は以下のサイトを参考にさせていただいた。
作成したプログラムを以下に載せる。
計算結果を確認する
とりあえず今回作成プログラムに問題がないか、参考元と同じパラメータを設定して結果を確認する。
参考元の\(R_0\)=2.0のパターンと同じ条件で計算した結果、以下のようなグラフが得られた。
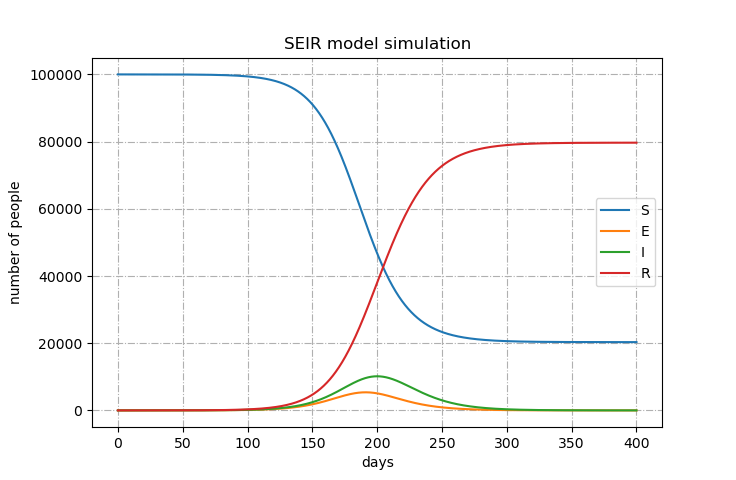
大体同じ結果が得られていそうなのでよしとする。
次に、先ほど検討したパラメータを設定して再度計算を行う。
\(R_0\)=1.5の場合
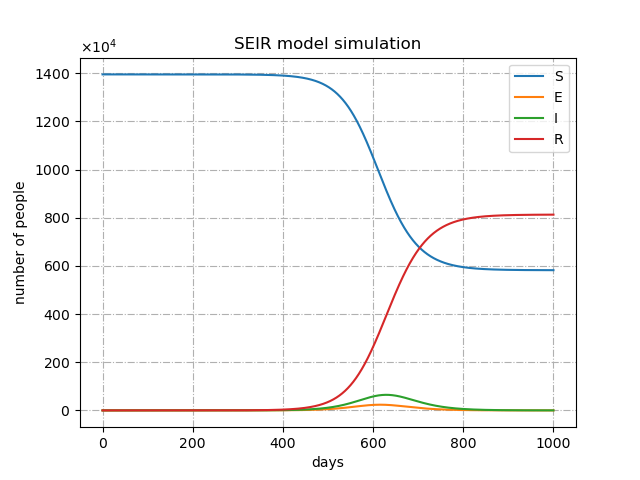
\(R_0\)=1.95の場合
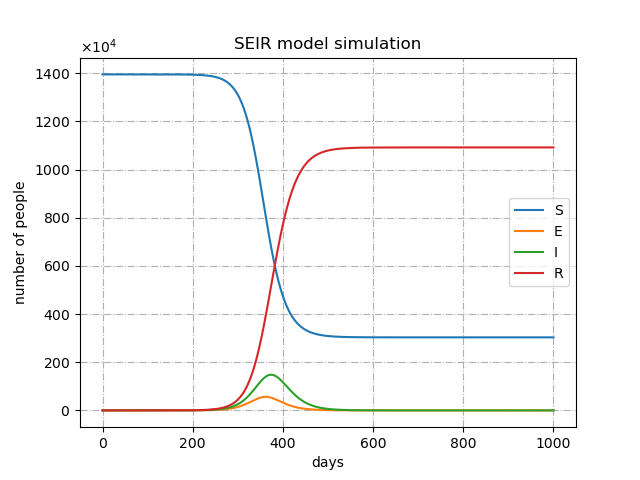
\(R_0\)=3.0の場合
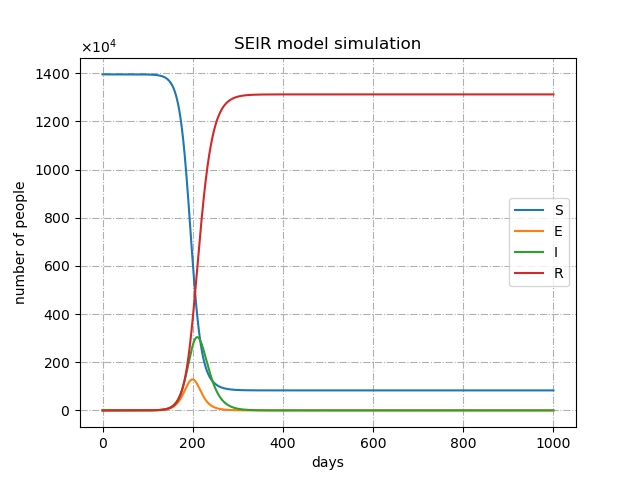
\(R_0\)が大きい(感染力が強い、人と人の接触率が高い)ほど
- ピークが急激
- 罹患者数が多い
- 収束が早い
という結果になるようだ。
雑記
久しぶりに数値計算のコードを書いたが、やはり数値計算は対象とする現象への理解が重要だなと思った。 今回に関しても、コードを作成している時間よりも、パラメータ設定のための調査の方に時間がかかった。
今回の感染症について調べてみて、色々なところが調査結果を出していることが改めて分かった。
また、ネットに落ちている情報としては予防や感染までの情報が多く、感染後の情報は比較的少ないと感じた。
-
reproductive number of COVID-19 is higher compared to SARS coronavirus | Journal of Travel Medicine | Oxford Academic ↩︎
-
The Incubation Period of COVID-19 From Publicly Reported Confirmed Cases | Annals of Internal Medicine | American College of Physicians ↩︎
-
新型コロナウイルス感染症(COVID-19 infection)|症状からアプローチするインバウンド感染症への対応~東京2020大会にむけて~ - 感染症クイック・リファレンス|日本感染症学会 ↩︎
-
新型コロナ潜伏期間は平均「5.2日」 福井県が暫定値算出 入院日数は「15.7日間」(福井新聞ONLINE) - Yahoo!ニュース ↩︎
-
https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf ↩︎
-
感染症発生動向調査及び積極的疫学調査により報告された新型コロナウイルス感染症確定症例287例の記述疫学(2020年3月9日現在) ↩︎
